Основные тригонометрические функции и их расчет
Тригонометрия изучает зависимости между сторонами и углами треугольников. В основе лежат четыре функции: синус, косинус, тангенс и котангенс. Для их вычисления используются координаты точки на единичной окружности.
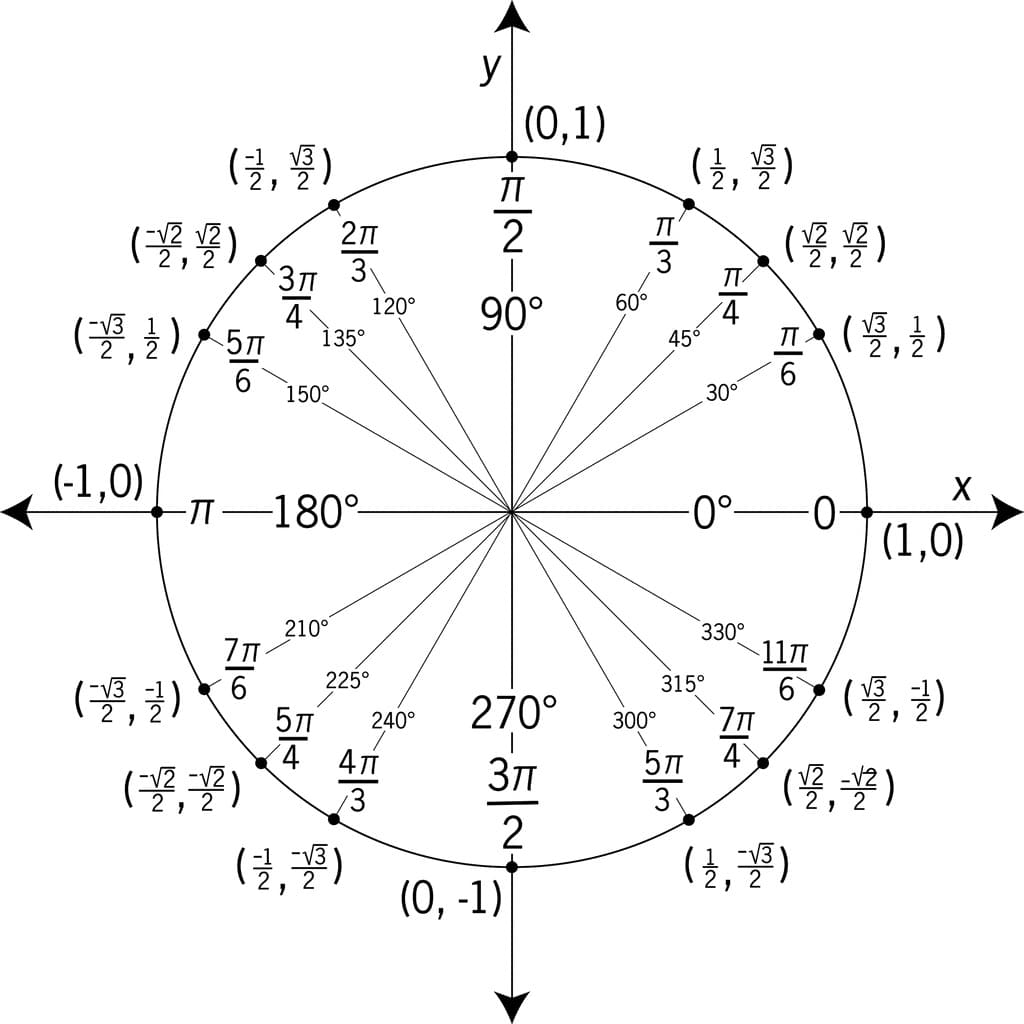
Связь между функциями
Функции связаны между собой фундаментальными тождествами:
Перевод единиц
Для перевода из градусов в радианы и обратно используйте формулы:
Таблица значений тригонометрических функций
В таблице приведены точные значения для наиболее часто используемых углов:
| Градусы (°) | Радианы (rad) | sin(α) | cos(α) | tan(α) | cot(α) |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | — |
| 30° | π/6 | 1/2 | √3/2 | √3/3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | √3/3 |
| 90° | π/2 | 1 | 0 | — | 0 |
| 180° | π | 0 | -1 | 0 | — |
| 270° | 3π/2 | -1 | 0 | — | 0 |
| 360° | 2π | 0 | 1 | 0 | — |
Практическое применение
Расчет синусов и косинусов необходим при проектировании лестниц, расчете нагрузок на балки и даже при оценке траекторий в навигации. Если вы занимаетесь инженерными расчетами, вам также может быть полезен таможенный калькулятор для ввоза оборудования или расчет стоимости часа для оценки работы специалистов.